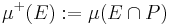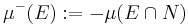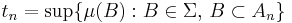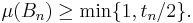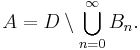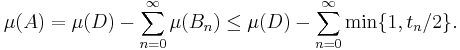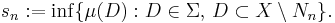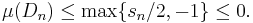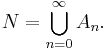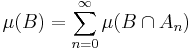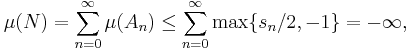Hahn decomposition theorem

In mathematics, the Hahn decomposition theorem, named after the Austrian mathematician Hans Hahn, states that given a measurable space (X,Σ) and a signed measure μ defined on the σ-algebra Σ, there exist two sets P and N in Σ such that:

P ∪ N = X and P ∩ N = ∅.
For each E in Σ such that E ⊆ P one has μ(E) ≥ 0; that is, P is a positive set for μ.
For each E in Σ such that E ⊆ N one has μ(E) ≤ 0; that is, N is a negative set for μ.

Moreover, this decomposition is essentially unique, in the sense that for any other pair (P', N') of measurable sets fulfilling the above three conditions, the symmetric differences P Δ P' and N Δ N' are μ-null sets in the strong sense that every measurable subset of them has zero measure. The pair (P,N) is called a Hahn decomposition of the signed measure μ.

Hahn–Jordan decomposition

A consequence of this theorem is the Jordan decomposition theorem, which states that every signed measure μ can be expressed as a difference of two positive measures μ⁺ and μ^–, at least one of which is finite; μ⁺ and μ^– are called the positive and negative part of μ, respectively. The two measures can be defined as

$\mu^%2B(E):=\mu(E\cap P)\,$

and

$\mu^-(E):=-\mu(E\cap N)\,$

for every E in Σ, and it is an easy task to verify that both μ⁺ and μ^– are positive measures on the space (X,Σ), at least one of them is finite (since μ cannot take both +∞ and −∞ as values), and satisfy μ = μ⁺ − μ^–. The pair (μ⁺, μ^–) is called a Jordan decomposition (or sometimes Hahn–Jordan decomposition) of μ.

Proof of the Hahn decomposition theorem

Preparation: Assume that μ does not take the value −∞ (otherwise decompose according to −μ). As mentioned above, a negative set is a set A in Σ such that μ(B) ≤ 0 for every B in Σ which is a subset of A.

Claim: Suppose that a set D in Σ satisfies μ(D) ≤ 0. Then there is a negative set A ⊆ D such that μ(A) ≤ μ(D).

Proof of the claim: Define A₀ = D. Inductively assume for a natural number n that A_n ⊆ D has been constructed. Let

$t_n=\sup\{\mu(B): B\in\Sigma,\, B\subset A_n\}$

denote the supremum of μ(B) for all the measurable subsets B of A_n. This supremum might a priori be infinite. Since the empty set ∅ is a possible B in the definition of t_n and μ(∅) = 0, we have t_n ≥ 0. By definition of t_n there exists a B_n ⊆ A_n in Σ satisfying

$\mu(B_n)\ge \min\{1,t_n/2\}.$

Set A_n+1 = A_n \ B_n to finish the induction step. Define

$A=D\setminus\bigcup_{n=0}^\infty B_n.$

Since the sets (B_n)_n≥0 are disjoint subsets of D, it follows from the sigma additivity of the signed measure μ that

$\mu(A)=\mu(D)-\sum_{n=0}^\infty\mu(B_n)\le\mu(D)-\sum_{n=0}^\infty\min\{1,t_n/2\}.$

This shows that μ(A) ≤ μ(D). Assume A were not a negative set. That means there exists a B in Σ which is a subset of A and satisfies μ(B) > 0. Then t_n ≥ μ(B) for every n, hence the series on the right has to diverge to +∞, which means μ(A) = –∞, which is not allowed. Therefore, A must be a negative set.

Construction of the decomposition: Set N₀ = ∅. Inductively, given N_n, define

$s_n:=\inf\{\mu(D):D\in\Sigma,\, D\subset X\setminus N_n\}.$

as the infimum of μ(D) for all the measurable subsets D of X \ N_n. This infimum might a priori be –∞. Since the empty set is a possible D and μ(∅) = 0, we have s_n ≤ 0. Hence there exists a D_n in Σ with D_n ⊆ X \ N_n and

$\mu(D_n)\le \max\{s_n/2, -1\}\le 0.$

By the claim above, there is a negative set A_n ⊆ D_n such that μ(A_n) ≤ μ(D_n). Define N_n+1 = N_n ∪ A_n to finish the induction step.

Define

$N=\bigcup_{n=0}^\infty A_n.$

Since the sets (A_n)_n≥0 are disjoint, we have for every B ⊆ N in Σ that

$\mu(B)=\sum_{n=0}^\infty\mu(B\cap A_n)$

by the sigma additivity of μ. In particular, this shows that N is a negative set. Define P = X \ N. If P were not a positive set, there exists a D ⊆ P in Σ with μ(D) < 0. Then s_n ≤ μ(D) for all n and

$\mu(N)=\sum_{n=0}^\infty\mu(A_n)\le\sum_{n=0}^\infty\max\{s_n/2, -1\}=-\infty,$

which is not allowed for μ. Therefore, P is a positive set.

Proof of the uniqueness statement: Suppose that 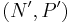$(N',P')$ is another Hahn decomposition of $X$ . Then $P\cap N'$ is a positive set and also a negative set. Therefore, every measurable subset of it has measure zero. The same applies to $N\cap P'$ . Since

$(P\,\triangle\,P')\cup (N\,\triangle\,N')=(P\cap N')\cup(N\cap P'),$

this completes the proof. Q.E.D.

External links

Hahn decomposition theorem at PlanetMath.